三体问题,竟被Transformer解决了?发现全局李雅普诺夫函数,已经困扰了数学家们132年。作为分析系统随时间稳定性的关键工具,李雅普诺夫函数有助于预测动态系统行为,比如著名的天体力学三体问题。
它是天体力学中的基本力学模型,指三个质量、初始位置和初始速度都是任意的可视为质点的天体,在相互之间万有引力作用下的运动规律问题。
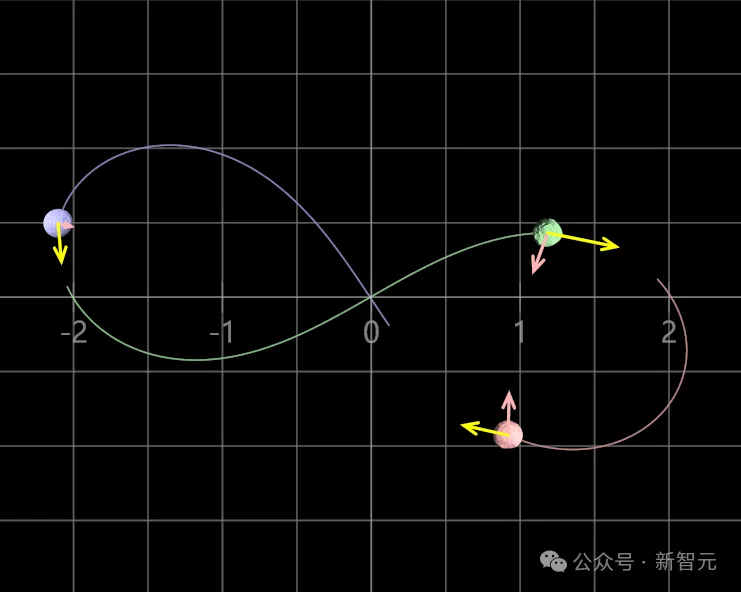
现在已知,三体问题不能精确求解,无法预测所有三体问题的数学情景。(「三体人」的困境,就是三体问题的一个极端案例。)现在,Meta AI解决了这个问题。目前,论文已被NeurIPS 2024接收。

论文地址:https://arxiv.org/abs/2410.08304今天,论文发布十几天后,AI社区再度被它刷屏。
 就在前一阵,苹果的一项研究引起广泛热议:LLM不具备推理能力,可能只是复杂的模式匹配器而已。有趣的是,这篇论文在结尾呼应了这个问题,做了极其精彩的论述——
就在前一阵,苹果的一项研究引起广泛热议:LLM不具备推理能力,可能只是复杂的模式匹配器而已。有趣的是,这篇论文在结尾呼应了这个问题,做了极其精彩的论述——
从逻辑和推理的角度来看,有人认为规划和高层次的推理可能是自回归Transformer架构的固有限制。然而,我们的研究结果表明,Transformer确实可以通过精心选择训练样本,而非更改架构,来学会解决一个人类通过推理解决的复杂符号数学问题。我们并不认为Transformer是在进行推理,而是它可能通过一种「超级直觉」来解决问题,这种直觉源自对数学问题的深刻理解。
虽然这个系统化的方法仍是一个黑箱,无法阐明Transformer的「思维过程」,但解决方案明确,且数学正确性可以得到验证。Meta研究者表示:生成式AI模型可以用于解决数学中的研究级问题,为数学家提供可能解的猜测。他们相信,这项研究是一个「AI解决数学开放问题」的蓝图。无论如何,陶哲轩和今天的这项研究都已证明,无论LLM究竟会不会推理,它都已经彻底改变数学这类基础科学的研究范式。那些在历史长河中的未解数学之谜,破解答案的一天或许已经离我们无比接近。
Transformer解决132年前数学难题
全局李亚普诺夫函数,控制着动力系统的稳定性。它会衡量一个开始接近平衡的系统,是否会始终保持接近平衡(或偏离平衡)?其中最著名的案例,就是「三体问题」了。
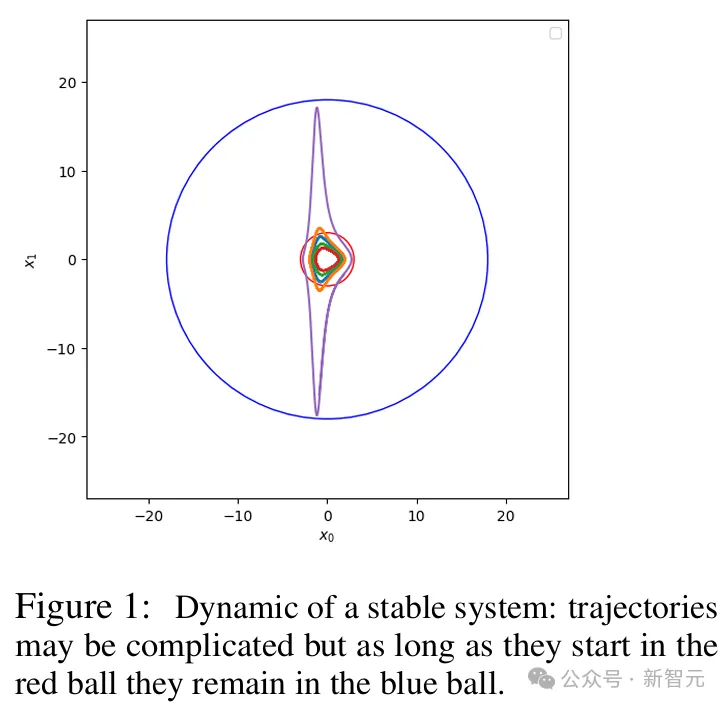
轨迹可能很复杂,但只要从红球开始,它们最终都会留在蓝球的位置1892年,李亚普诺夫证明,如果可以找到一个函数V,在平衡时具有严格的最小值,在无穷大时具有无限大,并且梯度始终指向远离系统梯度的方向,那么全局稳定性就能得到保证。遗憾的是,他未能提供寻找函数V的方法。好在,一百多年后,大模型出现了。以前,不存在寻找李亚普诺夫函数的通用方法,现在LLM是否能解决?研究者们惊喜地发现,自己的模型发现了两个稳定系统,以及相关的李雅普诺夫函数。

为此,Meta AI研究者引入一种后向生成技术来训练模型。这项技术根据Lyapunov函数创建动力系统,而这些系统的分布与我们实际想要解决的问题不同。尽管模型必须在分布外进行泛化,但使用逆向生成数据训练的模型,在可以用数值工具求解的多项式系统测试集上仍能取得良好的性能。

通过向后向训练集中添加少量(0.03%)简单且可解决的“前向”示例,性能就得到极大提高。这种「启动模型」大大优于最先进的方法。
在稳定性未知的一组随机动力系统上,研究者测试了自己的模型,发现在10%到13%的情况下,都能找到新的新的李亚普诺夫函数。
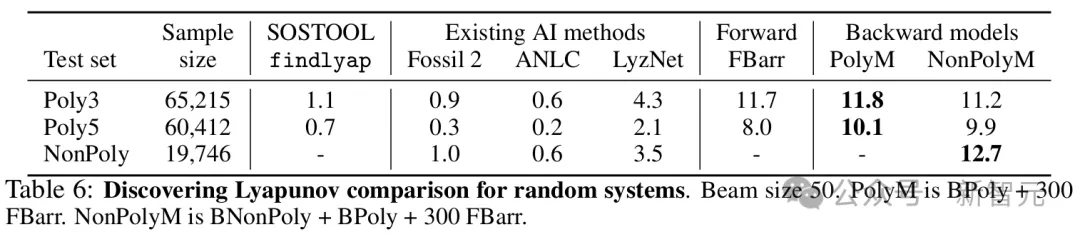
在这项任务上,这些增强的模型在各种基准测试中大大超越了最先进的技术和人类表现。它们的准确率超过80%,但硕士生级别的人类数学家在这项任务上的准确率不到10%。最后,研究者测试了模型在随机生成系统中发现未知李雅普诺夫函数的能力。在多项式系统中(当前方法唯一能解决的系统),模型为10.1%的系统找到了李雅普诺夫函数,而最先进的技术仅为2.1%。在非多项式系统中(当前没有已知算法),最佳模型为12.7%的系统发现了新的李雅普诺夫函数。
系统稳定性与李雅普诺夫函数
发现控制动力系统全局稳定性的李雅普诺夫函数,是一个长期存在但易于形式化的数学开放问题。这个函数代表着当时间趋于无穷时,其解相对于平衡点或轨道的有界性。动力系统的稳定性是一个复杂的数学问题,吸引了许多代数学家的兴趣,从18世纪的牛顿和拉格朗日,到20世纪研究三体问题的庞加莱。
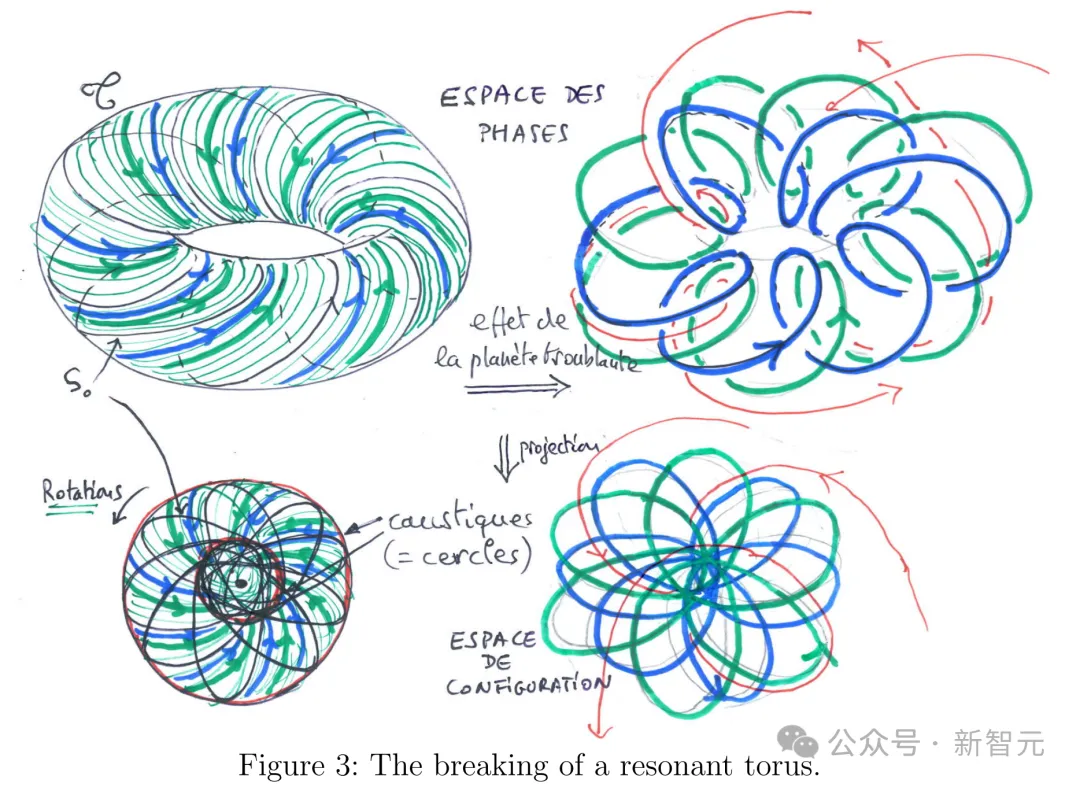
评估稳定性的主要数学工具是由李雅普诺夫提出的,他在1892年证明,如果可以找到一个递减的类似熵的函数——李雅普诺夫函数,那么系统就是稳定的。

系统稳定性
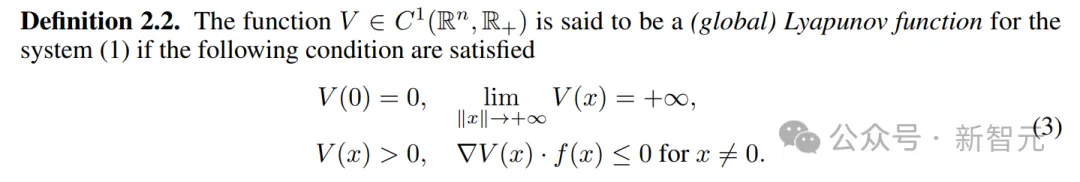
全局渐进稳定性后来,李雅普诺夫函数的存在被证明是大系统稳定性的必要条件。

不幸的是,目前尚无已知方法可以在一般情况下推导出李雅普诺夫函数,已知的李雅普诺夫函数仅适用于少数系统。事实上,130年后,系统推导全局李雅普诺夫函数的方法仅在少数特殊情况下已知,而在一般情况下的推导仍然是一个著名的开放问题。为此,研究者提出了一种从随机采样的李雅普诺夫函数中生成训练数据的新技术。在这些数据集上训练的大语言模型中的序列到序列Transformer,在保留测试集上实现了接近完美的准确率(99%),并在分布外测试集上表现出很高的性能(73%)。
实验设置
在这项工作中,研究者训练了序列到序列的Transformer,来预测给定系统的李雅普诺夫函数(如果存在)。他们将问题框定为翻译任务:问题和解决方案被表示为符号token的序列,模型从生成的系统和李雅普诺夫函数对中进行训练,以最小化预测序列与正确解决方案之间的交叉熵。为此,研究者训练了具有8层、10个注意力头和嵌入维度为640的Transformer,批大小为16个样本,使用Adam优化器,学习率为10^−4,初始线性预热阶段为10,000次优化步骤,并使用反平方根调度。所有实验在8个32GB内存的V100 GPU上运行,每个epoch处理240万样本,共进行3到4个epoch。每个GPU的训练时间在12到15小时之间。
数据生成
研究者将模型在大型数据集上进行训练和测试,这些数据集由稳定系统及其相关的李雅普诺夫函数对组成。采样此类稳定系统有两个难点。首先,大多数动力系统是不稳定的,并且没有通用的方法可以决定一个系统是否稳定。其次,一旦采样到一个稳定系统,除了特定情况下,没有通用的技术可以找到李雅普诺夫函数。在本文中,研究者依赖于反向生成,通过采样解决方案并生成相关问题来处理一般情况,以及正向生成,通过采样系统并使用求解器计算其解决方案,来处理小度数的可处理多项式系统。
反向生成
反向生成方法,从解决方案中采样问题,只有在模型能够避免学习逆转生成过程或“读取”生成问题中的解决方案时才有用。例如,当训练模型解决求整数多项式根的难题时,人们可以轻松从其根(3、5、7)生成多项式:
![]()
然而,如果模型是从P(X)的因式分解形式进行训练的,它将学会读取问题的根,而非计算它们。另一方面,简化形式
![]()
也并未提供任何线索。反向生成的第二个困难是,对解决方案而非问题进行采样,会使训练分布产生偏差。为此,研究者提出了一种从随机李雅普诺夫函数V生成稳定系统S的过程。

经过以上六步,产生了一个稳定系统S:ẋ=f(x),其中V作为其Lyapunov函数。
正向生成
尽管在一般情况下稳定性问题尚未解决,但当多项式系统的李雅普诺夫函数存在并可以写成多项式的平方和时,已有方法可以计算这些函数。这些多项式复杂度的算法对于小型系统非常高效,但随着系统规模的增长,其CPU和内存需求会急剧增加。研究者利用这项算法,来生成前向数据集。
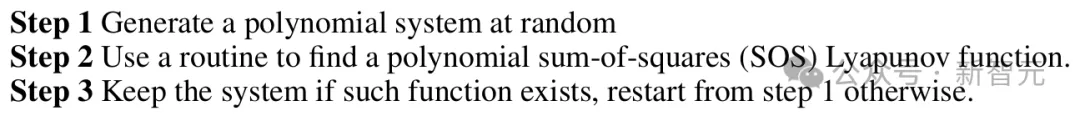
这种方法也有几个局限性,限制了该方法可以解决的多项式系统的类别。
数据集
研究者生成了两个用于训练和评估目的的反向数据集和两个正向数据集,以及一个较小的正向数据集用于评估目的。

结果
研究者在不同数据集上训练的模型,在保留测试集上取得了接近完美的准确率,并且在分布外测试集上表现非常出色,特别是在用少量正向示例增强训练集时。它们大大超越了当前最先进的技术,并且还能发现新系统的李雅普诺夫函数。以下是这些结果的详细信息。
分布内和分布外的准确率
在本节中,研究者展示了在4个数据集上训练的模型的性能。所有模型在域内测试中都取得了高准确率,即在它们训练所用数据集的留出测试集上进行测试时。在正向数据集上,障碍函数预测的准确率超过90%,李雅普诺夫函数的准确率超过80%。在反向数据集上,训练于BPoly的数据集的模型几乎达到了100%的准确率。研究者注意到,束搜索,即允许对解进行多次猜测,显著提高了性能(对于表现较差的模型,束大小为50时提升了7到10%)。在所有后续实验中,研究者都使用了50的束大小。

对生成数据训练的模型的试金石,是其分布外(OOD)泛化能力。所有反向模型在测试正向生成的随机多项式系统(具有平方和李雅普诺夫函数)时,都取得了高准确率(73%到75%)。最佳性能由非多项式系统(BNonPoly)实现,这是最多样化的训练集。反向模型在具有障碍函数的正向生成系统集(FBarr)上的较低准确率,可能是因为许多障碍函数不一定是李雅普诺夫函数。在这些测试集上,反向模型必须应对不同的分布和略有不同的任务。另一方面,正向模型在反向测试集上的表现较差。这可能是由于这些训练集的规模较小。总体而言,这些结果似乎证实了反向训练的模型并未学习反转其生成过程。如果是这样,它们在正向测试集上的表现将接近于零。它们还显示了良好的OOD准确率。

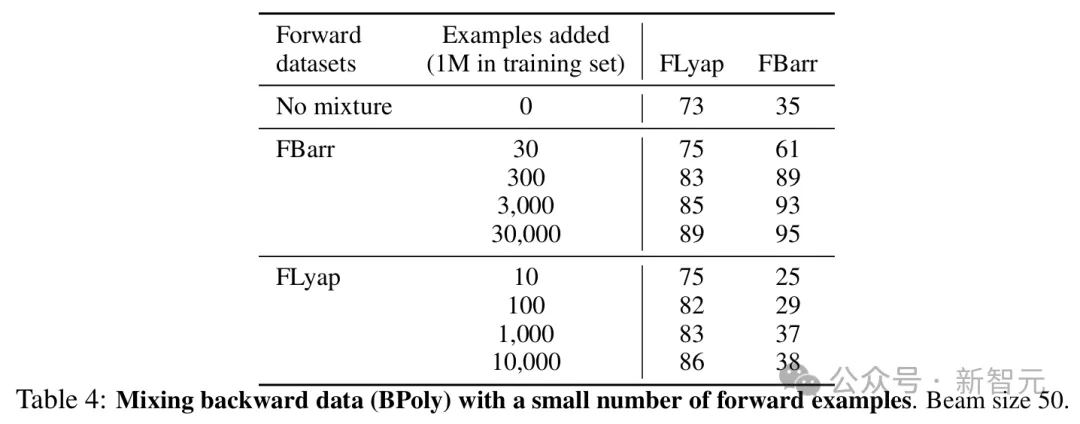
通过丰富训练分布来提高性能
为了提高反向模型的OOD性能,研究者在其训练集中加入了一小部分正向生成的示例。值得注意的是,这带来了显著的性能提升。将300个来自FBarr的示例添加到BPoly中后,FBarr的准确率从35%提高到89%(尽管训练集中正向示例的比例仅为0.03%),并使FLyap的OOD准确率提高了10多个百分点。从FLyap添加示例带来的改进较小。这些结果表明,在反向生成数据上训练的模型的OOD性能,可以通过在训练集中加入少量我们知道如何解决的示例(几十或几百个)来大大提高。在这里,额外的示例解决了一个较弱但相关的问题:发现障碍函数。因为所需示例数量很少,因而这种技术特别具有成本效益。
与当前最先进的基线比较
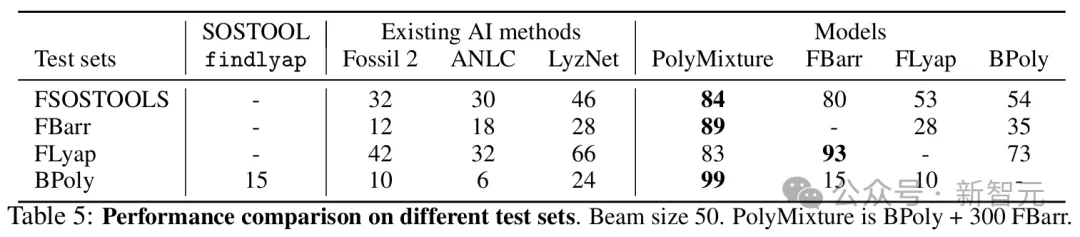
为了给模型提供基线,研究者开发了findlyap,这是MATLAB的SOSTOOLS中的李雅普诺夫函数查找器的Python对应版本。他们还引入了FSOSTOOLS,这是一个包含1500个整数系数多项式系统的测试集,具有SOSTOOLS可以求解的整数系数。研究者还测试了基于AI的工具,例如Fossil 2、ANLC v2和LyzNet。这些方法在测试集上取得了较低的准确率。这可能是因为这些工具旨在解决不同的问题:发现局部或半全局李雅普诺夫函数(并可能寻找控制函数),而研究者的目标是全局李雅普诺夫函数。表5比较了findlyap和基于AI的工具以及研究者模型在所有可用测试集上的表现。
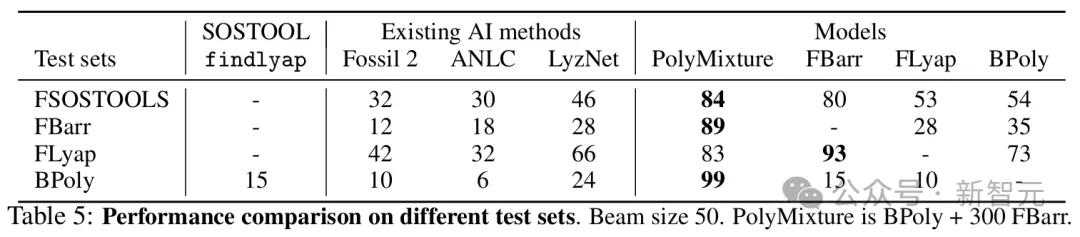
一个在BPoly上训练并补充了500个来自FBarr的系统的模型(PolyMixture)在FSOSTOOLS上达到了84%的准确率,证实了混合模型的高OOD准确率。在所有生成的测试集上,PolyMixture的准确率都超过了84%,而findlyap在反向生成的测试集上仅达到了15%。这表明,在多项式系统上,从反向生成数据训练的Transformer模型,相比于之前的最先进技术取得了非常强的结果。平均而言,基于Transformer的模型也比SOS方法快得多。当尝试解决一个包含2到5个方程的随机多项式系统时,findlyap平均需要935.2秒(超时为2400秒)。对于研究者的模型,使用贪婪解码进行一个系统的推理和验证平均需要2.6秒,使用束大小为50时需要13.9秒。
探索未知领域:发现新的数学
这次研究的最终目标,就是发现新的李雅普诺夫函数。为了测试模型发现新的李雅普诺夫函数的能力,研究者生成了三个随机系统的数据集:
– 包含2或3个方程的多项式系统(Poly3)
– 包含2到5个方程的多项式系统(Poly5)
– 包含2或3个方程的非多项式系统(NonPoly)对于每个数据集,生成100,000个随机系统,并消除那些在x^∗ = 0处局部指数不稳定的系统,因为系统的雅可比矩阵具有实部严格为正的特征值。然后,将findlyap和基于AI的方法与两个在多项式系统上训练的模型进行比较:FBarr和PolyM(ixture)——BPoly与来自FBarr的300个示例的混合——以及一个在BPoly、BNonPoly和来自FBarr的300个示例的混合上训练的模型(NonPolyM)。在多项式数据集上,最佳模型(PolyM)为11.8%和10.1%的(3阶和5阶)系统发现了李雅普诺夫函数,比findlyap多出十倍。对于非多项式系统,李雅普诺夫函数在12.7%的示例中被找到。这些结果表明,从生成的数据集和李雅普诺夫函数训练的大语言模型确实能够发现尚未知的李雅普诺夫函数,并且表现远高于当前最先进的SOS求解器。
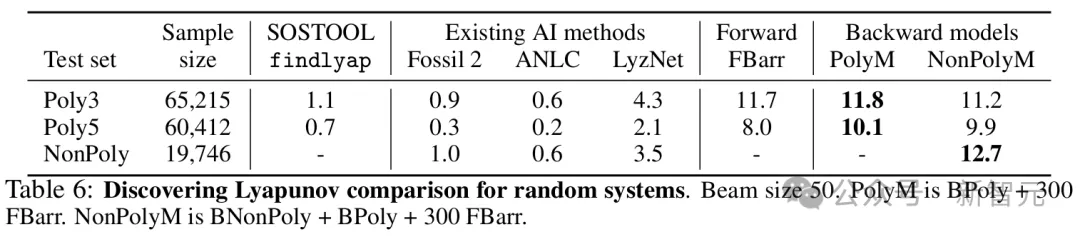
模型找到正确解决方案的百分比
专家迭代
接下来,研究者为多项式系统创建了一个经过验证的模型预测样本,FIntoTheWild,将其添加到原始训练样本中,并继续训练模型。
n1:添加20,600个样本,分别来自BPoly(20,000)、FBarr(50)、FLyap(50)和FIntoTheWild(500)
n2:添加2,000个样本,分别来自FLyap(1,000)和FIntoTheWild(1,000)
n3:添加50个来自FIntoTheWild的样本
n4:添加1,000个来自FIntoTheWild的样本
n5:添加2,000个来自FIntoTheWild的样本
n6:添加5,000个来自FIntoTheWild的样本此外,研究者还从头开始重新训练一个模型(n7),使用BPoly(1M)、FBarr(500)、FLyap(500)和FIntoTheWild(2,000)的混合。
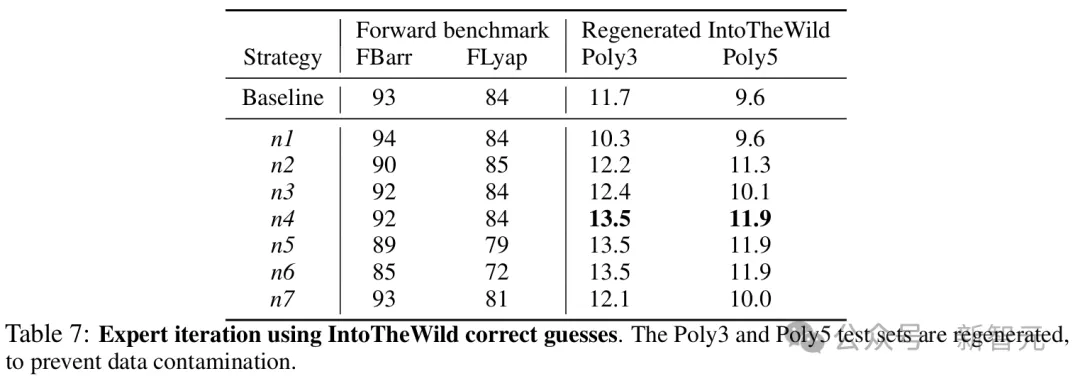
不同微调策略下,模型在前向基准和「探索未知领域」中的表现可以看到,向100万训练集添加1,000个经过验证的预测可将「探索未知领域」测试集的性能提高约15%,同时不会影响其他测试集(n4)。而添加更多样本似乎是有害的,因为它降低了其他基准的性能(n5和n6)。此外,使用来自其他分布的混合数据进行微调效率不高(n1和n2),而少量贡献已经有助于取得一些改进(n3)。最后,从头开始使用FIntoTheWild的数据预训练模型效率不高(n7)。
Transformer不会推理,但有「超级直觉」
这项研究已经证明,模型可以通过生成的数据集进行训练,以解决发现稳定动力系统的李雅普诺夫函数。对于随机多项式系统,研究者的最佳模型可以在五倍于现有最先进方法的情况下,发现李雅普诺夫函数。它们还可以发现非多项式系统的李雅普诺夫函数(目前尚无已知算法),并且能够重新发现由Ahmadi等人发现的多项式系统的非多项式李雅普诺夫函数。
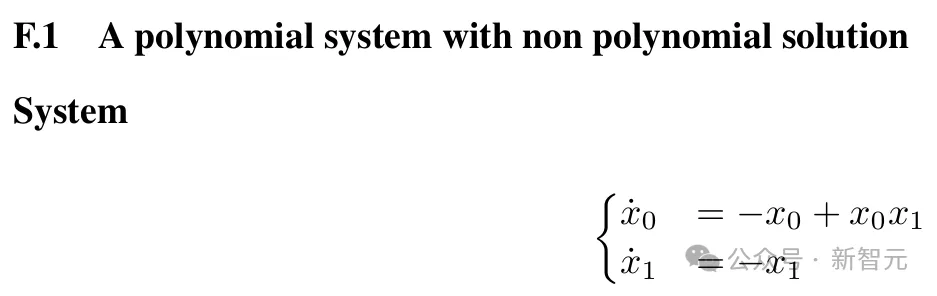

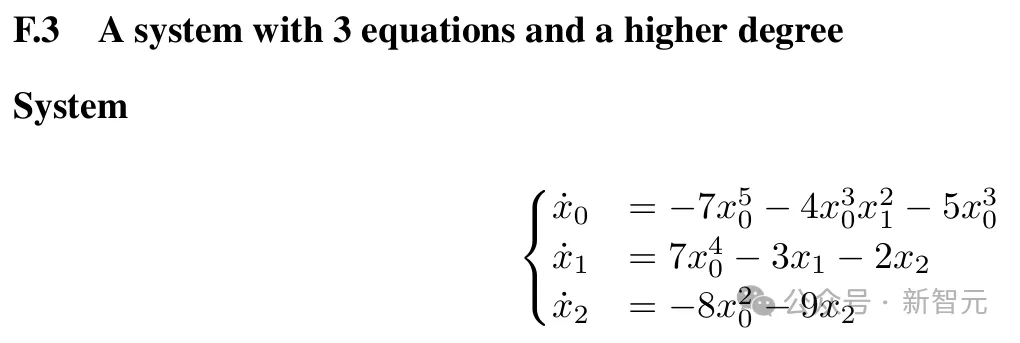
研究者也承认,工作仍有一些局限性。由于没有已知的方法来判断随机系统是否稳定,他们缺乏非多项式系统的良好基准。此外,本文研究的所有系统都相对较小,多项式系统最多为5个方程,非多项式最多为3个方程。他们相信,扩展到更大的模型应该有助于处理更大、更复杂的系统。最后,这项工作可以扩展到考虑非多项式系统的定义域。总之,这项工作在两个方向上具有更广泛的影响:Transformer的推理能力,以及AI在科学发现中的潜在作用。









暂无评论内容